درهم تنیدگی کوانتومی به زبان ساده

از تونل زنی در موانع نفوذناپذیر گرفته تا حضور همزمان در دو مکان مجزا، جهان کوانتومی اتمها و ذرات بسیار حیرت آفرین است. یکی از ویژگیهای جذاب دنیای کوانتوم “درهم تنیدگی” (Entanglement) کوانتومی است.ویژگی که در سالهای آینده تأثیری بسیار ژرف بر حوزه ارتباطات و امنیت اطلاعات خواهد گذاشت. اگرچه درهم تنیدگی کوانتومی یکی از عجیب ترین موضوعات دنیای علم است با این وجود موضوعات زیربنایی آن ساده هم است.هنگامی که این موضوعات فهمیده شوند، درهم تنیدگی فهم غنی تری را از مفاهیمی چون “چند جهانی” (Many worlds) نظریه کوانتوم را ممکن می سازد.
در این مطلب که چکیده ی یکی از آثار فیزیکدانان بزرگ معاصر بنام فرانک آنتونی ویلچک (استاد MIT و یکی از برندگان نوبل فیزیک 2004) است سعی شده با زبانی بسیار ساده به موضوعات زیربنایی درهم تنیدگی کوانتومی پرداخته شود. درهم تنیدگی کوانتومی اغلب بعنوان یک پدیده ای منحصر به مکانیک کوانتومی در نظر گرفته می شود، حال آنکه اینطور نیست. در واقع، برای فهم این مطلب بهتر است ابتدا با زبانی کلاسیک ( غیرکوانتومی)، درهم تنیدگی را توضیح دهیم ( گرچه تا حدی نامتعارف است). این ما را قادر می سازد تا چیستی درهم تنیدگی را بهتر متوجه شویم و موقتأ آن را از دنیای پر رمز و راز کوانتوم خارج کنیم.
در هم تنیدگی کوانتومی در چه زمانی رخ میدهد؟
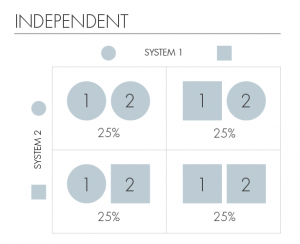
درهم تنیدگی در موقعیتهایی رخ میدهد که ما نسبت به حالت دو سیستم دانشی جزیی (Partial Knowledge) داریم. بعنوان مثال دو سیستم را در نظر بگیرید که میتوانند دو شی باشند که ما آنها را C-Sها مینامیم (S به سیستم و C به کلاسیک بودن آن اشاره دارد) برای درک راحتتر فرض کنید این C-Sها کیک هستند. C-Sهای ما (کیکها) میتوانند در دو شکل “مربع” و “دایره” باشند که ما آنها را حالتهای ممکنه C-Sها می نامیم. بنابراین ما میتوانیم برای دو C-S ( کیکها) چهار حالت ممکنه مشترک در نظر بگیریم. این حالات شامل (مربع، مربع)، (مربع، دایره)، (دایره، مربع) و (دایره، دایره) باشند.این دو سیستم می توانند مستقل یا وابسته به هم باشند.زمانیکه مامیگوییم C-Sها مستقل اند یعنی اینکه دانش ما از حالت یک سیستم ( دایره یا مربع بودن) اطلاعات مفیدی از حالت دیگری نمی دهد.جدول زیر به خوبی این خاصیت را نشان میدهد.
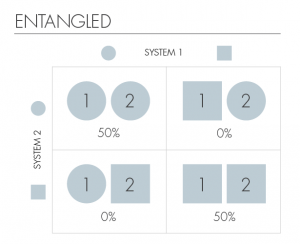
در سیستم بالا اگر شما بدانید یکی از C-Sها ( مثلأ کیک ها) دایره ای است هنوز با قاطعیت نمی توانید در خصوص شکل دومی اظهار نظر کنید. به طور مشابه، دانستن شکل دومی هیچ اطلاعات مفیدی در خصوص شکل اولی نمیدهد. از سوی دیگر ما میگوییم هر دو سیستم ما (C-Sها) درهم تنیدهاند (entangled) هنگامی که داشتن اطلاعات از یکی آگاهی ما از دیگری را بهبود دهد. جدول زیر به خوبی در هم تنیدگی کامل را نشان میدهد .
در این حالت، هر وقت که شکل اولین C-S دایره ای باشد ، ما میدانیم دومی نیز دایره ای است ( حالتی مشابه دارد).و هنگامی که اولی مربع باشد دومی نیز چنین خواهد بود. لذا با آگاهی از شکل یکی از انها، ما میتوانیم با قطعیت شکل دیگری را حدس بزنیم. تفسیر کوانتومی این موضوع نیز دارای ماهیتی کاملأ مشابه است. در تئوری کوانتوم، حالتها توسط اشیاء ریاضی به نام توابع موج (Wave Functions) توصیف میشوند. قواعدی که توابع موج را به احتمالات فیزیکی مرتبط می سازند از پیچیدگی های بسیار جالبی برخوردارند. همانگونه که در ادامه توضیح داده خواهد شد، مفهوم زیربنایی آن همچون مثال فوق ساده و روشن خواهد بود.
به عنوان نوعی از سیستم های ماکروسکپی(Macroscopic Systems)، کیک ها را نمی توان سیستم کوانتومی در نظر گرفت. با این وجود، ، درهم تنیدگی بین سیستمهای کوانتومی به طور طبیعی رخ می دهد.بعنوان نمونه، بعد از برخورد ذرات، آنها درهم تنیده میشوند. بنابراین، در عمل، حالات ناهم تنیده به ندرت وجود دارند. برای اینکه هر وقت که سیستم ها با هم اندرکنش (تعامل برقرار) می کنند، این اندرکنش همبستگی هایی در بین آنها ایجاد میکند. بعنوان نمونه، یک اتم را در نظر بگیرید، که خود از زیرسیستم هایی بنام الکترون و هسته( شامل پروتون و نوترون) متشکل شده است، پایین ترین حالت انرژی آن در واقع حالت بسیار درهم تنیده ای از الکترون ها و هسته است. به طوریکه مکان (position) این ذرات به هیچ وجه مستقل نیستند. (و) همانطور که هسته حرکت می کند، الکترون ها نیز با آن حرکت میکنند.
با بازگشت به مثال اصلی، اگر ما و
را بعنوان توابع موج توصیف کننده سیستم یک در حالتهای مربع یا دایره بنویسم و
و
را بعنوان توابع موج توصیف کننده سیستم دو در حالتهای مربع یا دایره بنویسم. سپس مثال عملیاتی ما را می تون به صورت های روابط (1) و (2) نوشت.
روشن است که ما می توانیم سیستم یک را به صورت رابطه(3)نیز بازنویسی کنیم. اگر توجه کنید متوجه خواهید شد که چگونه پرانتزهای موجود در این فرمول، به نحوی روشن سیستمهای یک و دو را در واحدهای مستقلی تفکیک داده است.
برای ایجاد حالات در هم تنیده (یعنی سیستم دو) ما روش های متعددی داریم .یک روش این است که سیستم مورد نظر را اندازه گیری (Measurement ) نماییم که این اطلاعات نسبی به ما می دهد. مثلأ شکل سیستم اول را مورد اندازهگیری قرار دهیم و شکل دوم را بر همین اساس حدس بزنیم.پیامدهای ممتاز درهم تنیدگی کوانتومی نظیر اثر انشتاین-پودولسکی-روزن (EPR ) در پیوند این مفهوم با مفهوم دیگری بنام “اصل مکملیت” (Complementarity) ایجاد شده اند. برای روشن سازی اثر (EPR ) بهتر است که در وهله نخست به معرفی “اصل مکملیت” بپردازیم.
پیشتر ما فرض کردیم که C-Sهای ما ( سیستمهای کلاسیک) می توانند دو شکل را نشان دهند ( مربه و دایره) . حال ما فرض میکنیم که آنها می توانند دو رنگ را نیز نشان دهند ( آبی و قرمز) اگر ما در خصوص سیستمهای کلاسیک صحبت کنیم مثل کیک ها، این خاصیت های افزوده جدید حاکی از آن خواهد بود که C-Sهای ما می توا نند در هر یک از چهار حالت ممکنه ی : یک مربع قرمز، یک دایره قرمز، یک مربع آبی یا یک دایره آبی باشند.حال فرض کنید که ما یک سیستم کوانتومی داریم بنام q-s ( که q به کوانتومی بودن سیستم (s) اشاره دارد) حال اگر کیک های ما q-s باشند در واقع ما با دو کیک کوانتومی روبرو هستیم. کیک های کوانتومی موقعیتی کاملأ متفاوت از کیک های کلاسیک ( مثال قبلی) دارند. این نکته به این واقعیت بر می گردد که اگر یک q-s در موقیعت های مختلف میتواند اشکال یا رنگ های متفاوتی را نشان دهد لزومأ به این معنا نیست که آن q-s هم یک شکل و یک رنگ را به صورتی آنی دارد . ما هنگامی که به اندازه گیری شکل q-sها می پردازیم عملأ تمامی اطلاعات مرتبط با رنگ آنها را از دست میدهیم. یا بر عکس اگر اقدام به اندازه گیری ( شناسایی) رنگ آنها بنماییم ما تمام اطلاعات مرتبط با شکل آنها را از دست خواهیم داد. مطابق با نظریه کوانتوم، ما نمیتوانیم شکل و رنگ یک q-s را به صورت آنی اندازه گیری کنیم. هیچ دیدگاهی از واقعیت فیزیکی تمام جنبه های آن را احصاء (Capture) نمی کند (لذا) فرد باید دیدگاههای متفاوت و متقابلی (Mutually exclusive) را اتخاذ نماید که هر یک اطلاعات معتبر اما جزیی از واقعیت را در اختیار او قرار میدهد. این چیزی که در قلب اصل مکملیت قرار دارد همانطور که نیلز بور آن را فرموله کرده است.
در نتیجه،نظریه کوانتوم ما را مجبور می سازد تا در تعیین ( و تقلیل) واقعیت های فیزیکی به خواص فردی دقت داشته باشیم. برای پرهیز از تضاد فکری ما باید بپذیریم که :
1: خاصیتی که اندازه گیری نمی شود نیازی نیست وجود داشته باشد ( توجه شود که این با نباید وجود داشته باشد فرق دارد)
2: خود اندازه گیری یک فرایند فعال است که سیستم تحت اندازه گیری را تحت تأثیر قرار میدهد.
حال عجیب بودن (strangeness) نظریه کوانتوم را به ارایه یک مثال کلاسیک (بهتر است بگوییم دور از کلاسیک) نشان میدهیم. این مثال در آزمایشات واقعی به صورت دقیق بررسی شده است ( در ازمایشات واقعی، محققان بجای اندازه گیری شکل یا رنگ کیک ها، مواردی چون تکانه ی زاویه ای الکترون را مورد اندازه گیری قرار می دهند).
آلبرت انشتاین، بوریس پودولسکی و ناثان روزن (EPR) یک اثر جالب را در این زمینه توصیف کردهاند. این اثر که از ان بعنوان اثر EPR یاد میشود هنگامی که ذرات به هم تنیده میگردند ایجاد میشود. این اثر در واقع شکل خاص ( و آزمایش پذیری) از درهم تنیدگی را با اصل مکملیت پیوند میدهد. فرض کنید یک جفت EPR شامل دو q-s است که هر یک از آنها یا برای شکلش یا رنگش ( نه هردو ) مورد اندازهگیری قرار میگیرد. فرض میکنیم که ما به بسیاری از این جفت ها دسترسی داریم که همه ی آنها یکسانند (Identical) و ما میتوانیم انتخاب کنیم که کدام خاصیت آنها اندازه گیری کنیم ( شکل یا رنگ). اگر ما شکل یکی از اعضای یک جفت EPR را اندازه گیری می کنیم ، آن با احتمال برابری یا دایره خواهد بود یا مربع و حال اگر رنگ آن را مورد اندازه گیری (شناسایی) قرار دهیم آن با احتمال برابری یا قرمز است یا آبی.
اثرات جالبی که انشتین و همکاران، آنها را پارادوکسیکال ( متناض نما) نامیدند زمانی رخ می دهند که ما اندازه گیری هایی از هر دو عضو یک جفت انجام دهیم. زمانیکه ما برای شناخت شکل یا رنگ هر دو عضو، اندازه گیری را انجام میدهیم همواره به نتایج سازگاری میرسیم. به نحوی که هر وقت رنگ عضو اول قرمز/آبی است به حتم رنگ دومی نیز قرمز/آبی خواهد بود و برای شکل نیز هر وقت شکل عضو اول دایره ای/مربعی است، شکل دوم نیز دایره ای/مربعی خواهد بود. از طرف دیگر، وقتی ما شکل یکی را اندازه گیری میکنیم و سپس اقدام به اندازهگیری رنگ دیگری میکنیم خواهیم دید که هیچ همبستگی وجود ندارد. یعنی اگر شکل اولی مربع باشد رنگ دومی با احتمال برابر یا قرمز خواهد بود یا آبی.
مطابق با مکانیک کوانتومی، حتی اگر بین این دو سیستم فاصله زیادی هم باشد و ما تقریبأ هم زمان آزمایشها را انجام دهیم باز به نتایج مشابهای خواهیم رسید. انتخاب اندازهگیری ( چه چیزی را اندازهگیری کنیم) به نظر میرسد روی سیستم دیگری که قرار است اندازهگیری شود اثر میگذارد. این چیزی است که انشتاین از آن بعنوان ” اقدام شبح وار در یک فاصله ” یاد میکرد. به نظر میرسد که در این وضعیت سرعت انتقال اطلاعات – از انچه مورد اندازه گیری قرار گرفته است- مستلزم نرخی بالاتر از سرعت نور است. اما آیا واقعأ چنین است؟ تا زمانی که من از نتیجه ای که شما بدست آورده اید آگاهی یابیم، من نمی دانم چه انتظار می رود(چه خواهد شد). من زمانی اطلاعات مفیدی کسب می کنم که نتیجه ای که شما اندازه گیری کرده اید را یاد بگیرم، نه در لحظه ای که شما آن را اندازه گیری می کنید. (لذا) هر پیامی که نتیجه اندازه گیری شما را آشکار می سازد باید از یک طریق فیزیکی مشخص انقال یابد که ( احتمالأ) نرخ آن از سرعت نور کمتر باشد.
منبع
https://www.quantamagazine.org/entanglement-made-simple-20160428/




خیلی عالی توضیح داده بودیدیکم از این کوانتوم سر در آوردم سپاس فراوان از شما
✔️ری استارت ✔️جواب سوالات بی پاسخ ❤️🌹
،اثبات وجود خدا با فیزیک ، آینده زندگی مرگ
راز های هستی حالت سوم نور در کانال تلگرامی ری استارت 🥰😍 با اجرای خوشگل سید محمد حسینی😇
✔️ری استارت ✔️جواب سوالات بی پاسخ ❤️🌹
،اثبات وجود خدا با فیزیک ، آینده زندگی مرگ
راز های هستی حالت سوم نور در کانال تلگرامی ری استارت 🥰😍 با اجرای خوشگل سید محمد حسینی😇 ممنون از وقتی که برای آگاهی دادن ما میذارید 🍻❤️
اصلا نفهمیدم😂😂😂
منم همینطور😐😂
✔️ری استارت ✔️جواب سوالات بی پاسخ ❤️🌹
،اثبات وجود خدا با فیزیک ، آینده زندگی مرگ
راز های هستی حالت سوم نور در کانال تلگرامی ری استارت 🥰😍 با اجرای خوشگل سید محمد حسینی😇