اعداد بی‌نظیرند. از همان کودکی که با اعداد آشنا می‌شویم دوست داریم بدانیم بزرگترین عدد دنیا چند است؟ اگر این سوال را امروز از ما بپرسند شاید بگوییم ∞ (بینهایت)، اما بینهایت اصلا یک عدد نیست! بلکه یک تئوری برای اثبات مواردی است که برای همیشه ادامه پیدا می‌کنند و هرگز پایان ندارند. پس بزرگترین عدد دنیا چند است؟ همانطور که می‌دانید برای این سوال هیچ جوابی وجود ندارد چون شما همیشه می‌توانید به هر عدد 1 اضافه کنید و آن را بزرگتر از قبل کنید. پس با این حساب من این سوال را به «بزرگترین عددی که می‌شناسیم چند است؟» تغییر می‌دهم تا به سوالی تبدیل شود که بتوان به آن پاسخ داد. این موضوع برای خود من بسیار جذاب بود و در همین زمینه کمی تحقیق کردم و نتیجه این بررسی‌ها را در این مطلب برای شما می‌نویسم.
میلیون
برای درک بهتر ماجرا از اعدادی شروع میکنم که از آن درک بهتری داریم و کم کم به سمت اعداد بزرگتر می‌رویم. فکر میکنم برای شروع 1 میلیون عدد خوبی باشد. همانطور که می‌دانید 1 میلیون شش صفر مقابل 1 دارد و به عبارتی دیگر 10 به توان 6 است. اگر تصمیم گرفتید از 1 تا 1 میلیون بشمارید بدانید که به 12 روز زمان نیاز دارید. ما با این عدد روزانه درگیر هستیم، ماشینی که می‌خریم یا خانه‌هایی که می‌خریم و خیلی چیزها با میلیون سروکار دارد اما اگر مثال نزدیک تر بزنیم همین صفحه لپ‌تاپ شما احتمالا یک میلیون یا حتی بیشتر پیکسل دارد. اگر رزولوشن مانیتور شما 1280 در 800 باشد در حال نگاه کردن به یک میلیون پیکسل هستید.
این مطلب را از دست ندهید : وسایل عجیبی که در پروازها ممنوع هستند
میلیارد و تریلیون
یک میلیون در مقایسه با یک میلیارد عدد بسیار کوچکی است. برای مثال شمردن 1 تا 1 میلیارد 32 سال طول می‌کشد! (که این کار را پیشنهاد نمی‌کنیم!) البته میلیارد هم عدد عجیبی نیست و در مکالمات روزمره ما استفاده میشود. برای مثال جمعیت کره زمین تقریبا 8 میلیارد نفر است، یا مثلا بیل گیتس 94 میلیارد دلار پول دارد. عدد بعدی یک تریلیون است. 1 تریلیون دوازده صفر مقابل یک دارد و شمردن از 1 تا 1 تریلیون بیشتر از 32 هزار سال زمان نیاز دارد! البته تریلیون هم تا حدودی کاربرد دارد. برای مثال تولید ناخالص داخلی آمریکا حدود 19 تریلیون دلار است.
*از اینجا به بعد دیگر برای ما خیلی کاربردی نیست و ممکن است حتی نام آنها را هم ندانیم.
این مطلب را از دست ندهید: زنبور عسل ریاضی می‌تواند بیاموزد!
کادریلیون، کوينتيليون و اکتیلیون
تریلیون در برابر کادریلیون عدد بزرگی نیست و البته خیلی هم کاربردی نیست اما دانستن این اعداد خالی از لطف نیست. کادریلیون پانزده صفر دارد و برای راحتی کار می‌گوییم با 10 به توان 15 برابر است. برای مثال روی زمین حدود 1 کادریلیون مورچه زندگی می‌کند. بعد از کادریلیون به کوينتيليون می‌رسیم که میشود 10 به توان 18 و برای مثال هر دانه نمک 1.2 کوينتيليون اتم دارد یا اگر همه ماسه‌های سواحل دنیا را بشمارید به چنین عددی می‌رسید. اگر این ماجرا را ادامه دهیم و از سکستیلیون و سپتیلیون هم بگذریم به اکتیلیون می‌رسیم که 10 به توان 27 است. برای مثال بدن هر انسان 7 اکتلیون اتم دارد.
حال همین ماجرا را باز هم ادامه می‌دهیم و به 10 به توان 80 می‌رسیم. این عدد به قدری بزرگ است گفته میشود تعداد کل اتم‌هایی است که در دنیا وجود دارد. برای درک بهتر یادآوری میکنم که تعداد اتم‌های بدن یک انسان از تعداد کل ماسه‌های سواحل دنیا بیشتر است. حالا تصور کنید در کل دنیا چه تعداد اتم وجود دارد. بله 10 به توان 80 اتم. این عدد بسیار بزرگ است اما در برابر اعدادی که ما می‌دانیم همچنان ناچیز است! از اینجا به بعد تصمیم داریم تا کمی درباره اعداد بزرگ صحبت کنیم!
عدد بعدی ما 1 گوگل (Googol) است. این عدد به لطف جست‌وجوگر گوگل برای ما آشنا است. البته نوشتار انگلیسی آن کمی متفاوت است. بزرگی یک گوگل به اندازه 10 به توان 100 است. پیدا کردن کاربرد برای این عدد به نظر کمی مشکل می‌آید زیرا اگر همه اتم‌های دنیا را هم بشمارید باز هم کمتر از 1 گوگل خواهد شد. اما اگر بخواهیم هرجوری شده این عدد را استفاده کنیم نیاز به یک مکعب روبیک 6 در 6 در 6 داریم. در این صورت خانه‌های این مکعب روبیک می‌توانند به 1.57 ضرب در 10 به توان 116 مدل مختلف در کنار هم قرار بگیرند، حالا این عدد حتی از یک گوگل هم بیشتر است.
در علم فیزیک واحد بسیار کوچکی برای اندازه‌گیری طول داریم به نام Planck که معادل 10 به توان منفی 35 متر است. برای اینکه متوجه کوچکی Planck بشوید باید بگوییم که سپتیلیون (10 به توان 24) بار از یک اتم کوچکتر است. حالا اگر بخواهیم همه دنیا را با جسمی که یک Planck طول دارد پر کنیم، 4 ضرب در 10 به توان 185 عدد از آن جسم نیاز داریم!
این مطلب را از دست ندهید : آمازون بزرگترین کارفرمای جهان
اعداد بی‌انتها هستند؟
حالا می‌خواهیم پا را از این هم فراتر بگذاریم! یاد گرفتیم که 10 به توان 100 برابر است با یک گوگل، پس اگر 10 را به توان 10 به توان صد برسانیم خواهیم داشت 10 به توان گوگل که به این عدد «گوگل پلکس» می‌گوییم. گوگل پلکس عددی است که گوگل (10 به توان 100) صفر مقابل یک دارد. کم کم توضیح دادن اعداد برای دانشمندان هم مشکل میشود. در واقع گوگل پلکس آنقدر بزرگ است که برای نوشتن آن روی کره زمین جای کافی وجود ندارد! اما ریاضیدانان دست بردار نیستند و این عدد را هم بزرگتر کرده‌اند. عدد بعدی یک «گوگل پلکسیان» است. این عدد یعنی 10 به توان 10 به توان 10 به توان 100 که یعنی به زبان ساده‌تر یعنی 10 به توان «گوگل پلکس». اما سعی نکنید تا متوجه شوید «گوگل پلکسیان» چقدر است به این دلیل که مغز انسان توان پردازش آن را ندارد. در تمام دنیا هم فضای مناسبی برای نوشتن این عدد وجود ندارد و اما اگر وجود داشت نوشتن این عدد تریلیون‌ها سال نوری زمان نیاز دارد.
مرتبط: حل سخت‌ترین مسایل ریاضی جهان توسط رایانه
اما آیا «گوگل پلکسیان» بزرگترین عددی است که بشر می‌شناسد؟ پاسخ شما خیر است! عدد بعدی که بشر پیدا کرده است عدد GRAHAM نام دارد. این عدد به نام ریاضیدان مشهور رونالد گراهام نام‌گذاری شده است. در عدد گراهام به‌جای توان ما از «↑» یا فلش روبه‌بالا استفاده می‌کنیم. این روش کمی اوضاع را تغییر می‌دهد برای مثال 3↑3 میشود 27 که درواقع همان 3 به توان 3 است. تا اینجا ساده است اما اگر داشته باشیم 3↑↑3 میشود 3 به توان 3 به توان 3 که عددی نزدیک به 7.6 تریلیون است. با این روش می‌توان بزرگترین اعداد دنیا را نوشت. برای مثال اگر بنویسیم 3↑↑↑3 این یعنی 3↑↑3↑↑3 که برای حساب کردن آن باید 3 را 7.6 تریلیون بار به توان 3 برسانیم. حال تصور کنید 3↑↑↑↑3 چه عدد بزرگی خواهد شد. حتی سعی نکنید این عدد را تصور کنید چون مغز انسان چنین قابلیتی ندارد! از این عجیب‌تر این است که ما هنوز به عدد گراهام نزدیک هم نشده‌ایم. بیاید به عدد بسیار بزرگ و باورنکردنی 3↑↑↑↑3 بگوییم G1 و حالا می‌خواهیم G2 را به دست بیاوریم. برای به دست آوردن G2 نیاز داریم تا ابتدا و انتها یک 3 بنویسیم و سپس به تعداد G1 فلش را میان این دوتا 3 قرار دهیم. به همین ترتیب برای به دست آوردن G3 نیاز داریم تا میان دوتا 3 به اندازه G2 فلش قرار دهیم. این عدد را آنقدر ادامه بدهید تا به G64 برسید که درواقع G63 فلش میان دوتا 3 دارد و این عدد گراهام است.
مرتبط: تصاویری از بزرگترین هواپیمای جهان
عدد گراهام به قدری بزرگ است که نه میشود آن را توضیح داد نه ذهن انسان یا حتی کامپیوتر قدرت پردازش چنین عددی را دارد. اما جالب است بدانید که حتی عدد گراهام هم بزرگترین عدیدی نیست که بشر می‌شناسد. اعداد بسیاری را بشر معرفی کرده که از عدد گراهام هم بزرگتر است. مانند TREE{3} و یا عدد Skewes و یا عدد Loader اما بزرگترین عددی که تا به حال بشر شناخته که از همه این اعداد هم بسیار بزرگتر است عدد RAYO نام دارد. عدد Rayo در یک مسابقه‌ای که دانشگاه MIT برگزار کرد به دست آمده است. این رقابت میان دو ریاضیدان بزرگ به نام‌های Augustin Rayo و Adam Elga برگزار شد و Rayo موفق شد بزرگترین عدد را با استفاده از علم ریاضی بنویسد. این عدد آنقدر بزرگ است که عدد گراهام در برابر آن صفر است و من حتی کلمه مناسبی برای توضیح آن پیدا نکردم. به همین دلیل لینک مطلب اصلی را می‌گذارم تا خود Rayo این عدد را واضح‌تر توضیح بدهد. درضمن جایزه این مسابقه هم یک میلیون دلار بود که Rayo آن را برنده شد. برای شنیدن مصاحبه او روی تصویر زیر کلیک کنید.
canadian pharmacy meds canadian pharmacy
male erection pills: gnc ed pills – best male enhancement pills
amoxicillin 875 mg tablet amoxicillin 500 mg tablets – over the counter amoxicillin
canada pharmacy online canadianpharmacyworld com
sabrina carpenter dating: dating seiten uster – free adult date sites
من مطئنم كه واقعا عدد رايو هيچ جا كاربرد نداره. از خودت چرت و پرت نگو
همين الان من ميتونم يه عدد بزرگتر از رايو درست كنم
رايو به توان خودش
نه
منظور برج توانيه . يعني اول سه رو به توان سه برسون بعد سه رو به توان حاصل اينا كن. يعني اولويت از بالاست نه از پايين. سه به توان 27 چيزي نزديك به همون مقداره
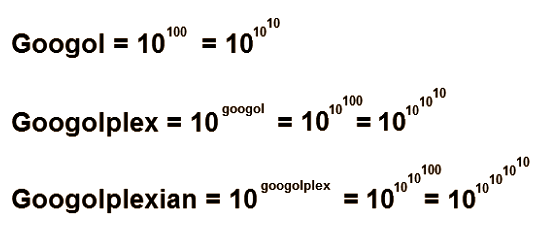
۱+۱=؟
نخبه ها جواب بدن همو پیدا کنیم
3
خیلی خوب بود ، ممنون
خیلی خوب بود ولی مغزم بالا نمیاره انقدر تو ذهنم صفر هارو تصور کردم مغزم حافظش پر شد هنگ کرد باید کل سیستمو پاک کنم از اول راه اندازیش کنم والاه
بزرگترین عدد جهان صفراست…خنده داراست اما واقعیته…🙏
واقعا صفره؟
دوست عزیز شما اشتباهی فاحش در محاسبات داشتید چطور ۳ بتوان ۳ بتوان ۳ میشود ۷ تیرلیون ؟ حتی اگر دبیرستان هم رفته باشید میدونید ک برا بدست آوردنش کافیه توان رو در هم ضرب کنی بعد بتوان عدد پایه برسونی . مطلب دوم اینکه این اعداد بعد از میلیارد کارایی ندارد و دونستن اسمش هم کمکی نمیکنه و در علم ریاضی و یا فیزیک اون رو با توان نشان میدن
۷٬۶۲۵٬۵۹۷٬۴۸۴٬۹۸۷
جواب 3 بتوان 3 بتوان3
۷
برای بی مغذی مثل تو کاربرد نداره وگرنه برای ریاضیدانان خیلی کاربردیه
درضمن منظورش 3 به توان 3 به توان 3 بدون پرانتز هست که میشه 3 به توان 27
برای تو که مطمئنا کاربردی نداره.
تو انگشتاتم بشماری تهش 3 & 4 تا اضافه میذاری، اینا که جای خود…
.
کسانی که دوست دارن بدونن که این اعداد ب چه دردی میخورن؟
جوابش : برای محاسبه احتمالات که هیچ حد و مرزی نداره.شایدم ی عده بگن که محاسبه این جور چیزا به چ دردی میخوره؟
برای کشف ، شناخت ، تسلط و بکارگیری هر چیزی، باید ابتدا محاسبات ریاضی رو ، روش انجام بدیم.
همین گوشی های هوشمندی که امروزه تو دست اکثر مردم هست، در هنگامی که دارید ازش استفاده میکنید، داره ثانیهای صدها میلیارد و گاهی تریلیون ها محاسبه رو انجام میده تا به شما خدمات بده (از پخش ی فیلم گرفته تا گرفتن عکس و …)
بشر 500 سال پیش کی فکرشو میکرد که دستگاهی فراگیر بسازه که قادر باشه تا ثانیه ای 20 تریلیون محاسبه درخواست شده ازش رو ب صورت بی وقفه انجام بده…؟؟!!
(منظورم محاسبات باینری یا همون {0 و 1} که اساس کار کامپیوترها و… به این شکل هست که هنوز هم داره 2 وجهی صورت میگیره.
حالا کی میتونه بفهمه که 500 یا 1000 سال دیگه این محاسبات به چ شکل و چ عددی خواهند رسید؟؟!!
این مثال کوچیکی بود از دنیای خیلی وسیع کاربرد اعداد.
گر تو بهتر می‌زنی بِستان نویس! چرا مقاله‌ی به این زیبایی را خط خطی میکنید؟
ممنون خیلی آموزنده و جذاب بود مغزم هنگ کرده نمیتونم حتی نظرمو بگم ممنون از سایتتون
اولا خسته نباشید من به عنوان یک آدم معمولی نیاز اطلاعاتیم را از مطلب با لا بردم وبسیار برای من که نه وقت دنبال کردن مباحث ریاضی را دارم ونه حوصله ونه دانش آن بسیار مفید کوتاه وآگاهی دهنده بود با تمام احترام نظردهندگان عزیز دیگر وبه حمایت از نگارنده عرض میکنم اینترنت نه آکادمی است نه آموزشگاه و نه هیچ نوع مرجع سیستماتیک آموزشی پس مباحث وزین علمی تخصصی در محدود افرادی خاص است وخرده گیری به نویسنده که با هنر بیان ساده وروان واستدلال گویا نیاز درک عامه مردمی که میل به درک وفهم بزرگترین وکوچکترین اعداد شناخته شده توسط بشر را دارند تامین کرده است وچقدر خوب بود ما بجای ضدیت وبرچسب زدن نیاز مردم عادی را محترم می شمردیم به امید روزی که از یک دیگر برای آگاهی دادن هرچند ساده و روان فهم قدردانی وسپاسگزار باشیم.
ما که نوشتیم چون انتقاد بود منتشر نکردید
ولی واقعیت اینه که متاسفانه این یک مقاله
عوام پسند و کم ارزش است که ارتباط چندانی
با ریاضی ندارد خوب حالا شما منتشر نکنید ،
مشکلی وجود ندارد ، سطح آگاهی مردم یک
کشور جهان چهارمی در همین حد شما و
شما در حد آنها (شامل خودم) هستید ، خوب
بتازید .
شما که جهان اولی اینجا چیکار میکنی؟
یک دیشلیارد
حس میکنم میشناسمت این عدد رو وقتی میگیم که گل زده باشیم و خیلی های شده باشیم و اون های بودن رو به اسم خط صدا میزنیم مثلا وقتی گل میکشی بعد نیم ساعت ازت میپرسیم خطت چنده تو میگی یک زوگیلیارد یا یوخیلماخ و یا دیشیلیارد و یا بالاترین خط سیکیلدیمیارد ، خط زیاد هستش 😂
واقعا نفهمیدم چی میگه
زشته
آیا در دانشگاه این اعداد هست؟
حیف …
بنظرم من صد سال زود بدنیا اومدم چه پیشرفت هایی که نخواهم دید تصور اینکه بشر چه مرزهای رو فتح میکنه دیوانه کننده است
خدا از سر سقراط نگذره ..
ما همه بدبدخيتم . من مال هزار سال بعد بودم . خدا اشتباهي منو الان افريد
چرا سقراط؟؟! 🙄🙄
میشه واضح بگین آخرین عدد دنیا بقیر از بی نهایت چیه ☹️🤔
سال 2029
اسم توچیه
بگو وقبل از بینهایت چیه
1
بینهایت منهای یک😂
بینهایت
بی نهایت منهای یک
پس اینهمه عدد های بزرگ وجود داشته؟
بسیار سپاسگزارم بابت معرفی اعداد گوگل پلکس و و بخصوص گراهام که عدد مورد علاقه من است و در باره آن تحقیقاتی کرده ام و همچنین عدد رایوو به دلیل خاص دیگری که اینجا مجال توضیح آن نیست ، ولی یکی دو تا خواهش دارم ، اول اینکه لطفا هنگام نوشتن مطالب لطفا دقت بیشتری بفرمایند به جای سال ننویسید سال نوری ، همگان به خوبی می دانند که سال نوری واحد طول است و نه زمان خم ،دوم اینکه ای کاش میلیون را اینهمه کوچک تصور نمی کردید ، ارزش بسیار پایین پول ملی ما باعث شده که میلیون بازیچه کودکان تلقی شود ولی خوب است بدانیم یک میلیون تعداد تارهای موی سر ده انسان بطور متوسط است، مطالب دیگری هم هست که متاسفانه مجال نیست ولی هنوز مهمترین موضوع باقی مانده ،
این اعداد بزرگی که معرفی کردید در واقع از جریان اصلی ریاضیات خیلی دور هستند و تقریبا کاربردی ندارند، برای مثال عدد گراهام پاسخ یک مساله ریاضی است و نه چیزی بیشتر و عدد رای و هم چنانکه فرمودید صرفا حاصل یک کری خوانی است و آنهم کاربردی (منظورم از کاربرد ، کاربرد در خود ریاضی است و نه تکنولوژی یا چیز دیگر) در واقع این اعداد بیشتر مناسب مقاله ها و نوشته های عامه پسند مانند همین مقاله حاضر می باشند.
این را هم عرض کنم هر عدد طبیعی هر چه هم بزرگ باشد تعداد اعداد طبیعی کوچکتر از خودش در برابر تعداد اعداد بزرگتر ، صفر است ، در ریاضی اگر یک مجموعه بی نهایت عضوی (بی نهایت شمارش پذیر که د ر واقع کوچکترین بی نهایت است ، چرا که تنها یک بی نهایت وجود ندارد و تعداد بی نهایت ها باز خود بی نهایت تاست کاش مجال برای توضیح و معرفی بی نهایت ها و تریبون بین آنها وجود داشت) اگر یک مجموعه.بی نهایت عضوی به اندازه رای و عضو آن خاصیتی را نداشته باشند و باقی اعضای مجموعه آن خاصیت را داشته باشند اصطلاح می گوییم که این مجموعه تقریبا همه جا این خاصیت را دارد و توجهی به بزرگی تعداد اعضای فاقد آن خاصیت نمی کنیم ، البته در ریاضی کلمه باوجود ندا د و این کلمه تقریبا در اینجا معنای دقیق ریاضی دارد که قبلا بوسیله تعریفی کاملا دقیق معنای آن را مشخص کرده ایم
بازدار باشید
عجب حوصله ای داری
یک گراهام
الو